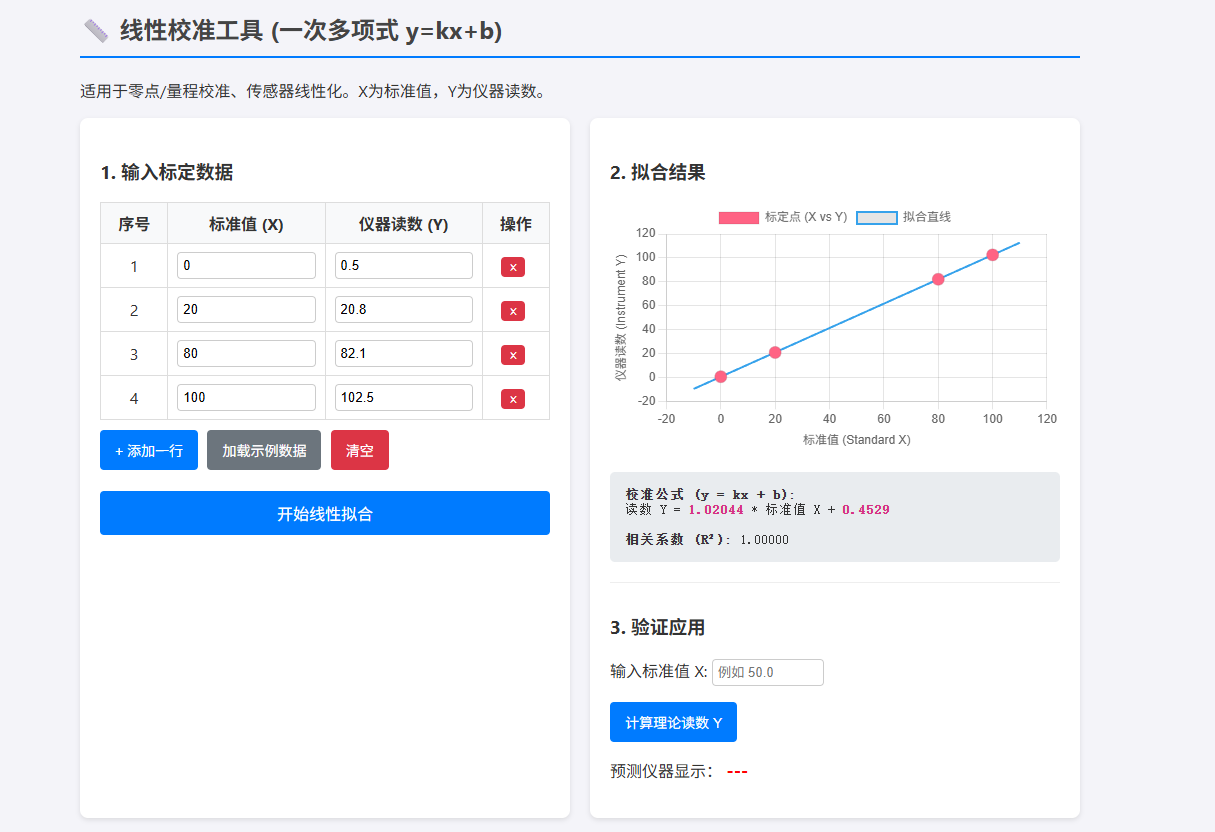
本篇继 [[流量计校准实现过程]],这里学习一次多项式拟合
工业分析仪中常见的“零点校准”和“量程(满度)校准”,本质上就是只有两个样本点的“一次多项式拟合”(线性回归)。
数学上,这就是在解一个二元一次方程组,求出直线方程 $y = kx + b$ 中的两个参数:
- $b$ (截距/Offset):对应 零点 (Zero)。
- $k$ (斜率/Slope):对应 量程/灵敏度 (Span/Sensitivity)。
不过,虽然数学本质一样,但在工程实现和操作逻辑上,普通的“零点/量程校准”和标准的“最小二乘法”有一点微妙的区别。我来为你拆解一下:
1. 数学本质:确定解 vs. 统计解
场景 A:两点校准(Zero & Span)—— “钉钉子”
这是大多数分析仪(如 CEMS 中的 $\text{SO}_2, \text{NO}_x$ 分析仪)的做法。因为只有两个点(零气点、标气点),两点确定一条直线。
- 步骤 1(通零气): 输入 $x=0$,测得 $y_{raw}$。
- 直接算出截距 $b = 0 - y_{raw}$(或者将当前的读数强行置为 0)。
- 这就像把直线的起点用钉子钉死在原点。
- 步骤 2(通标气): 输入 $x=Span$,测得 $y_{raw}$。
- 基于确定的 $b$,算出斜率 $k$。
- 这就像以零点为轴心,旋转这根线,直到它穿过标气点。
结论:这是一个代数计算过程,算出来的线必须完美经过这两个点。误差为 0(在校准那一刻)。
场景 B:最小二乘法(Least Squares)—— “找平衡”
这是你在配气仪或高精度流量计中用的方法(点数 $N > 2$)。如果你通了零气、20% 浓度、50% 浓度、80% 浓度、100% 浓度。
- 直线可能不会完美穿过零点,也不会完美穿过 100% 点。
- 它是一条“妥协”的线,试图让所有点的综合误差最小。
为什么工业分析仪偏爱“零点 + 量程”而不是“多点拟合”
既然多点拟合更准,为什么像西门子、赛默飞这些分析仪平时维护只做 Zero/Span?
原因一:漂移的物理意义不同
在传感器领域,误差通常来源于两个独立的物理现象,正好对应 $b$ 和 $k$:
- 零点漂移 (Zero Drift) $\rightarrow b$ 的变化
- 物理原因:电子元器件的热噪声、光电倍增管(PMT)的暗电流、背景光的干扰。
- 特点:它是一个叠加在所有读数上的固定值。
- 对策:只要每天通一次零气,把这个“底色”扣掉就行。
- 量程漂移 (Span Drift) $\rightarrow k$ 的变化
- 物理原因:紫外灯老化光强减弱、气体室镜片脏了、检测器灵敏度下降。
- 特点:它影响的是变化的比例。
- 对策:通入高浓度标气,重新计算放大倍数。
因为这两种漂移的机理不同,所以在仪表软件里,通常允许独立校准:
- 你可以只做零点校准(修正 $b$),而不动斜率 $k$。
- 这在最小二乘法里很难做到,因为一旦重新拟合,$k$ 和 $b$ 通常都会变。
原因二:法规与成本
- 成本:做多点线性化(Linearization)需要购买不同浓度的标气,或者使用昂贵的配气仪。
- 法规:如果每天都要做 5 点校准,运维人员会疯掉,标气成本也受不了。
模型的选择
如上所说,在常见的线性传感器领域,误差通常来源于两个独立的物理现象,正好对应 $b$ 和 $k$。对于非线性传感器,可能就需要选择二次多项式拟合(如 [[流量计校准实现过程]] 中所说的最小二乘法多项式拟合)
1、物理原理:金氏定律
热式流量计的核心原理是测量气体带走热量的速度。描述这一物理过程的经典公式是 King’s Law(金氏定律):$$P = I^2 R = A + B \cdot (Q)^n$$
- $P$:加热功率(对应传感器的输出电压或电桥电压 $V$)。
- $Q$:质量流量。
- $n$:指数常数,通常在 0.4 ~ 0.5 之间。
这意味着什么? 这意味着传感器输出的电压 $V$ 和流量 $Q$ 之间,根本不是直线关系,而是一个类似于 “根号曲线” 或 “对数曲线” 的关系。
- 在小流量区:散热极快,电压变化非常剧烈(灵敏度极高,曲线很陡)。
- 在大流量区:散热趋于饱和,电压变化变慢(灵敏度下降,曲线变平缓)。
如果你强行用一条直线(一次方程)去拟合这种“前陡后平”的物理曲线,误差会非常大——要么小流量测不准,要么大流量偏差巨大。
2、数学特性:泰勒级数展开
虽然 King’s Law 是指数关系,但在数学上,任何光滑的非线性函数,都可以在局部范围内展开成多项式(泰勒级数)。$$f(x) \approx a_0 + a_1x + a_2x^2 + a_3x^3 + \dots$$ 对于热式流量计这种单调变化(不回头、不震荡)的曲线,二次($x^2$)或三次($x^3$)多项式 恰好能完美地模拟由于指数 $n$ 带来的弯曲度。
- 二次项 ($ax^2$):提供了曲线的“弯曲方向”,让拟合线能顺着金氏定律的趋势“弯”过去。
- 最小二乘法:能够在这个弯曲的过程中,让所有标定点的整体误差(均方差)最小,自动平衡高低流量段的偏差。
3、工程需求:宽量程比 (High Turndown Ratio)
热式流量计的一个显著优点是量程比极宽,通常能达到 100:1 甚至更高(例如能测 5000 mL/min,也能测 50 mL/min)。
- 线性拟合的死穴:在 100:1 的宽量程下,直线完全无法兼顾首尾。
- 多项式拟合的优势:
- 它允许变斜率(Variable Slope)。
- 在低端,多项式的切线斜率大,匹配高灵敏度。
- 在高端,多项式的切线斜率小,匹配饱和区。