之前我们聊的“滑动平均”和“自适应滤波”,本质上都是“事后诸葛亮”(基于过去的数据来推测现在)。今天认识一位“预言家” —— 卡尔曼滤波 (Kalman Filter)。
它是阿波罗登月飞船导航的核心算法,也是现在自动驾驶汽车、大疆无人机悬停不动的秘密。在高端仪器(如 TDLAS 分析仪)中,它是解决“响应速度 (T90)”与“读数稳定性”这对死敌的唯一解药。
一、 核心哲学:你相信“理论”还是相信“眼睛”?
卡尔曼滤波最牛的地方在于,它不单纯依赖传感器,而是结合了两个信息源。
想象你在开车进隧道,GPS 信号突然变弱了(噪声变大)。
- 传感器(眼睛): GPS 告诉你:“你现在在坐标 (100, 50)……不对,下一秒在 (100, 500)……不对,在 (100, -20)。” —— 数据不可靠,乱跳。
- 物理模型(理论): 你的车速表显示 100km/h,方向盘没动。根据牛顿定律,你下一秒应该只前进了 27 米。
卡尔曼的灵魂追问: 此刻,你信谁?
- 如果是普通滤波:它会傻傻地把 GPS 的乱跳值取平均,结果你的车在地图上乱飞。
- 卡尔曼滤波:它会算出一个“信任权重” (Kalman Gain, $K$)**。
- 它发现 GPS 噪声(方差)太大了,于是屏蔽掉 90% 的 GPS 数据。
- 它选择相信 90% 的物理模型(根据上一秒位置 + 车速算出来的位置)。
- 结果: 哪怕 GPS 信号烂成渣,你的车在地图上依然画出了一条平滑的直线。
二、 CEMS 里的实战:如何消灭滞后?
在 CEMS 分析仪中,我们面临一个痛点:
- 为了让读数稳,我们加了很重的滤波(电容大,积分时间长)。
- 后果: 气体浓度真的突变时(比如喷氨了),读数慢吞吞地爬坡,T90 响应时间超标。
卡尔曼怎么解决?
- 建立模型(Predict):
- 仪器内部知道气体流速和管路体积。
- 它预测:如果进气口浓度变了,传感器腔室里的浓度应该按什么曲线变化(指数上升)。
- 测量修正(Update):
- 融合:
- 当实测值突然跳变,且跳变趋势符合流体力学模型时 $\to$ 卡尔曼说:“这是真信号,不是噪声!信任实测值,立刻跟进!”
- 当实测值跳变,但完全违背物理模型(比如 1ms 内变了 50%) $\to$ 卡尔曼说:“这不科学,肯定是干扰(Spike)。无视它,相信模型!”
最终效果: 平时稳如老狗(滤除噪声),变时动如脱兔(T90 极快)。
三、 Python 实战:手搓一个 1D 卡尔曼滤波器
卡尔曼滤波的矩阵公式($P = FPF^T + Q$)看着很吓人,但对于单变量(只测一个浓度)的情况,它可以简化成5 行代码。
我们要模拟:一个真实的温度信号(平稳),中间突然被一个巨大的噪声干扰,看看卡尔曼能不能把它识别出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
import numpy as np
import matplotlib.pyplot as plt
# 配置中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# ==========================================
# 1. 模拟数据生成
# ==========================================
n_iter = 100
sz = (n_iter,) # 数组大小
x = 25.0 # 真实温度 (Constant)
# 真实值:一直是 25度
truth = np.full(sz, x)
# 观测值:真实值 + 严重的白噪声 (模拟传感器)
# 噪声标准差 sigma = 2.0 (抖动很大)
z = truth + np.random.normal(0, 2.0, sz)
# 在第 50 个点,加一个巨大的脉冲干扰 (Spike)
z[50] = 100.0
# ==========================================
# 2. 卡尔曼滤波初始化
# ==========================================
# 这里的参数是"玄学",需要根据物理系统去调
# Q: 过程噪声协方差 (Process Noise)
# 代表:你觉得物理世界本身有多不稳定?
# 设得极小 (1e-5),代表我相信物理世界是连续的,温度不会瞬变。
Q = 1e-5
# R: 测量噪声协方差 (Measurement Noise)
# 代表:你觉得你的传感器有多烂?
# 设得大 (0.1),代表传感器噪声很大,我不信它。
R = 0.1 ** 2
# 初始化状态
x_est = 0.0 # 初始估计值
P = 1.0 # 初始估计误差 (不确定性)
K = 0.0 # 卡尔曼增益 (信任度)
result_kalman = []
# ==========================================
# 3. 卡尔曼滤波主循环 (5步心法)
# ==========================================
for i in range(n_iter):
# --- 阶段 A: 预测 (Predict) ---
# 1. 预测状态: 既然是测恒温,我预测下一刻温度和这一刻一样
x_pred = x_est
# 2. 预测误差: 加上物理世界的不确定性
P_pred = P + Q
# --- 阶段 B: 更新 (Update) ---
# 3. 计算卡尔曼增益 (K): 权衡 预测误差 vs 传感器误差
# 如果传感器误差 R 很大,K 就会很小 (不信传感器)
K = P_pred / (P_pred + R)
# 4. 更新估计值: 核心公式!
# 新估计 = 预测值 + K * (实测值 - 预测值)
# K 决定了我们要接受多少"实测偏差"
x_est = x_pred + K * (z[i] - x_pred)
# 5. 更新误差: 这一轮做完了,我会变得更自信 (P变小)
P = (1 - K) * P_pred
result_kalman.append(x_est)
# ==========================================
# 4. 绘图对比
# ==========================================
plt.figure(figsize=(12, 6))
plt.plot(z, 'k.', label='传感器测量值 (带噪声+尖峰)', alpha=0.3)
plt.plot(truth, 'g-', label='真实值 (25℃)', linewidth=2)
plt.plot(result_kalman, 'r-', label='卡尔曼滤波结果', linewidth=2)
plt.title("卡尔曼滤波实战:从噪声中还原真相", fontsize=16)
plt.xlabel("时间点")
plt.ylabel("温度")
plt.legend()
plt.grid(True)
plt.show()
|
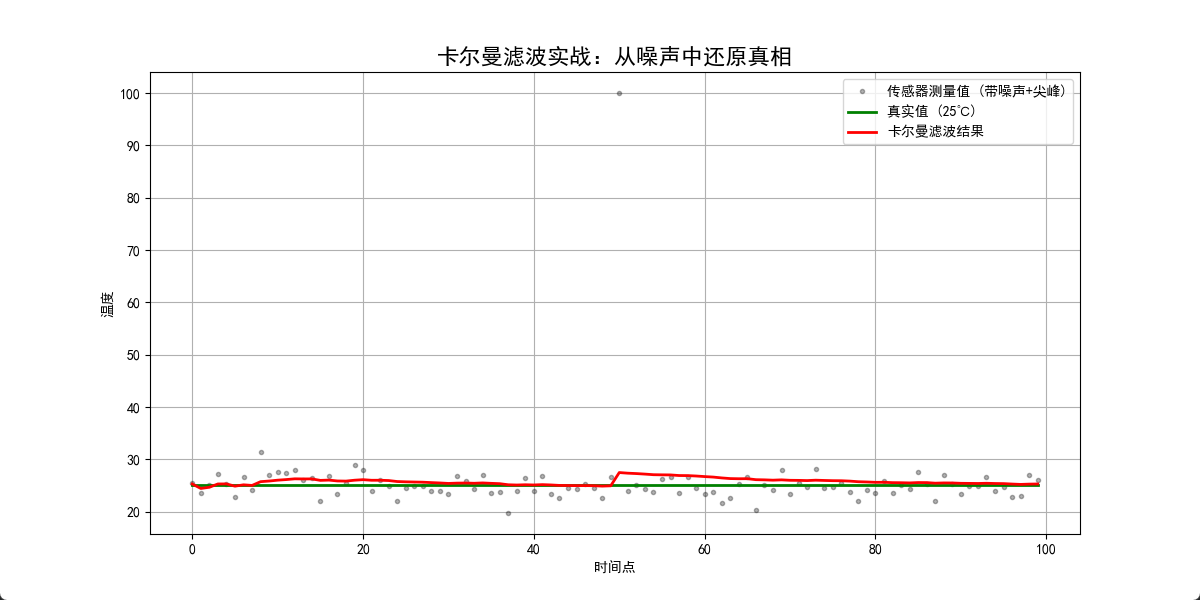
运行后的观察点
- 看整体: 尽管黑色的点(测量值)上下乱跳幅度很大,红色的线(卡尔曼)却非常平滑,紧贴着绿线(真实值)。这说明它滤除白噪声的能力极强。
- 看第 50 点(尖峰):
- 测量值瞬间跳到了 100。
- 卡尔曼滤波的红线仅仅微微向上动了一点点,甚至几乎没受影响。
- 原因: 因为我们设置了 $Q$ 很小。卡尔曼认为:“根据物理定律,温度不可能在 0.1 秒内从 25 度 变到 100 度。这肯定是传感器疯了。” 于是它通过极小的 $K$ 值,拒绝了这次“诈骗”。
四、 进阶:它比滑动平均强在哪?
你可能会问:“滑动平均也能滤除那个尖峰啊,为什么要搞这么复杂的公式?”主要区别在于“动态适应性”:
- 不确定性的动态追踪 ($P$ 值):**
- 刚开机时,卡尔曼知道自己“没底”($P$ 很大),它会非常听传感器的话($K$ 大),读数收敛极快。
- 运行一段时间后,它摸清了规律($P$ 变小),就开始变得“自信”,不再受噪声干扰。
- 滑动平均是死的,卡尔曼是活的。
- 多传感器融合 (Sensor Fusion):
- 这是卡尔曼的杀手锏。
- 如果你不仅有光电传感器,还有一个流速传感器。
- 你可以告诉卡尔曼:“流速变快了,所以浓度应该会变快。”
- 卡尔曼会利用流速信息,在光电传感器还没反应过来之前,就提前把浓度推上去。
- 这就是 Model-Based (基于模型) 的力量。
总结
- FFT 是用来找病因的(看成分)。
- PID 是用来做控制的(给动作)。
- 卡尔曼滤波 是用来做估计的(猜真相)。
