信号处理之清洗滤波

本篇继 [[信号处理的设计原则]]，具体学习清洗滤波层，怎么把输入的信号看清楚！

如果说物理获取层是“把矿石挖出来”，那么清洗滤波层就是“洗矿”——把泥巴（噪声）冲走，留下金子（信号）。在 CEMS 和精密仪器中，这一层通常由三道工序组成，针对三种不同类型的“脏东西”。

第一道工序：中值滤波 (Median Filter) —— 对付“捣乱分子”

敌人：脉冲噪声。比如：隔壁大电机启动了一下、继电器吸合打了个火花、或者是静电放电。特征：信号本来是 2.5V，突然变成 5.0V，下一毫秒又回到了 2.5V。

常规错误：用平均值。

数据：2.5, 2.5, 2.5, 50.0 (异常), 2.5
平均值：12.0。
后果：一个老鼠屎坏了一锅汤，平均值被瞬间拉高，DCS 显示瞬间超标。

正确解法：中值滤波（去头去尾）

算法：就像跳水比赛打分，去掉最高分，去掉最低分，剩下的取平均；或者直接取中间那个数。
中值： 2.5。
效果：那个 50.0 的异常值直接被扔进垃圾桶，对结果 0 影响。

第二道工序：IIR / FIR 低通滤波 —— 对付“背景嘈杂”

敌人：白噪声 (White Noise)。比如：电子热噪声、ADC 的量化误差。特征：像蚂蚁一样密密麻麻地附着在信号线上，让读数在小数点后几位乱跳。

主力武器： 滑动平均 (Moving Average) 或 指数加权平均 (EMA)。这两种算法在单片机里极其常见，我们重点看 EMA (指数移动平均)，因为它最省内存。公式：$$Y_{now} = \alpha \times X_{input} + (1 - \alpha) \times Y_{last}$$

$Y_{now}$：现在的输出。
$Y_{last}$：上一次的输出。
$X_{input}$：现在的 ADC 输入。
**$\alpha$ (滤波系数)： 0~1 之间的一个数。
- $\alpha$ 越小（如 0.01）：极度相信历史经验，不相信当前输入。效果：读数稳如泰山，但反应迟钝。
- $\alpha$ 越大（如 0.90）：** 极度相信当前输入，不看历史。效果： 反应极快，但读数乱跳。

第三道工序：自适应滤波 (Adaptive Filter) —— 解决“快与稳”的矛盾

这是这一层的大 BOSS。

痛点：

为了环保验收，T90 响应时间必须 < 200 秒 $\to$ 需要 $\alpha$ 大（弱滤波）。
为了数据好看，读数不能乱跳 $\to$ 需要 $\alpha$ 小（强滤波）。
矛盾：鱼和熊掌不可兼得。

解法：自适应（变档位）

算法会实时计算“当前的变化率”，然后自动调整 $\alpha$ 值。

静止状态：
- 算法发现：|当前值 - 上次值| < 阈值。
- 判断：现在工况很稳，波动都是噪声。
- 动作：切换到“重滤波模式”（$\alpha = 0.05$）。
- 结果：屏幕上的线条平滑得像直线。
突变状态：
- 算法发现：|当前值 - 上次值| > 阈值（比如突然喷氨了）。
- 判断：这不是噪声，是真变了！
- 动作：切换到“轻滤波模式”（$\alpha = 0.8$）甚至**“直通模式”**。
- 结果：读数“蹭”地一下就上去了，毫无滞后。

代码案例

写了一段代码，模拟一个从 0 跳变到 100 的信号，并加入噪声。我们将对比：普通平均 vs 自适应滤波。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63


import numpy as np
import matplotlib.pyplot as plt

# 配置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成模拟信号：0~50点是0，50点之后突变到100
t = np.arange(0, 100)
true_signal = np.zeros(100)
true_signal[50:] = 100

# 2. 加入严重的白噪声
np.random.seed(42)
noise = np.random.normal(0, 5, 100)
raw_signal = true_signal + noise

# 3. 定义两种滤波器

# --- 普通 EMA 滤波器 (固定系数) ---
def fixed_filter(data, alpha=0.1):
    output = np.zeros(len(data))
    output[0] = data[0]
    for i in range(1, len(data)):
        output[i] = alpha * data[i] + (1 - alpha) * output[i-1]
    return output

# --- 自适应滤波器 (智能系数) ---
def adaptive_filter(data):
    output = np.zeros(len(data))
    output[0] = data[0]
    
    # 核心逻辑
    for i in range(1, len(data)):
        # 计算变化量 (Delta)
        delta = abs(data[i] - output[i-1])
        
        # 自适应逻辑：如果变化量大，alpha就大；变化量小，alpha就小
        # 这里用一个简单的 sigmoid 或者是线性映射
        if delta > 10:  # 突变阈值
            alpha = 0.8 # 快反应
        else:
            alpha = 0.05 # 稳读数 (重滤波)
            
        output[i] = alpha * data[i] + (1 - alpha) * output[i-1]
    return output

# 4. 运行滤波
out_fixed = fixed_filter(raw_signal, alpha=0.1) # 固定系数
out_smart = adaptive_filter(raw_signal)         # 自适应

# 5. 画图对比
plt.figure(figsize=(12, 6))
plt.plot(raw_signal, 'k.', alpha=0.3, label='原始带噪信号')
plt.plot(true_signal, 'k--', alpha=0.5, label='真实值')

plt.plot(out_fixed, 'b-', linewidth=2, label='普通滤波 (反应慢)')
plt.plot(out_smart, 'r-', linewidth=2, label='自适应滤波 (又快又稳)')

plt.title("自适应滤波 vs 普通滤波", fontsize=16)
plt.legend(fontsize=12)
plt.grid(True)
plt.show()

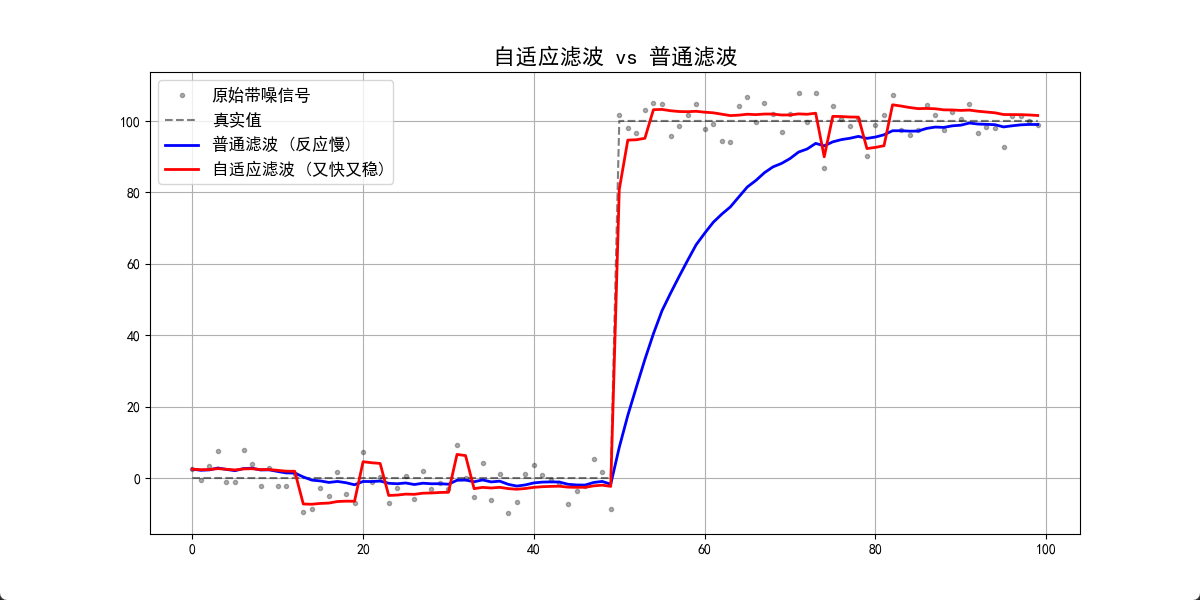
如果你运行这段代码，你会看到：

黑色点（原始数据）：上蹿下跳，根本没法看。
蓝线（普通滤波）：
- 优点：确实把噪声滤平了。
- 缺点：它是拖泥带水的。信号在第 50 秒已经跳到 100 了，蓝线在第 70 秒才慢悠悠地爬上来。这会导致 T90 不合格。
红线（自适应滤波）：
- 前半段（0）：非常平滑（因为它识别出没变化，用了重滤波）。
- 突变点（50）：瞬间跟上了信号的跳变（因为它识别出突变，扔掉了滤波器）。
- 后半段（100）：再次变平滑。

这就是“清洗滤波层”的最高境界：该稳的时候稳如老狗，该快的时候动如脱兔。