信号处理之频域分析

既然我们已经聊了 [[信号处理之清洗滤波]]（时域上的平均），今天我们要升级维度。我要带你进入信号处理的**“上帝视角”——频域分析 (Frequency Domain Analysis)。

我们要聊聊两个核心概念：FFT (快速傅里叶变换) 和 数字陷波器 (Notch Filter)。这能解决一个让无数工程师抓狂的问题：“我知道信号里有干扰，但我怎么知道干扰是从哪来的？我又该怎么精准地干掉它？”

第一章：从“看波形”到“看成分” —— FFT 的魔法

我们之前的示波器或绘图，都是“时域” (Time Domain) 的。

  • X 轴： 时间 (Time)
  • Y 轴： 电压 (Amplitude)
  • 看到的是： 一条乱糟糟的曲线。

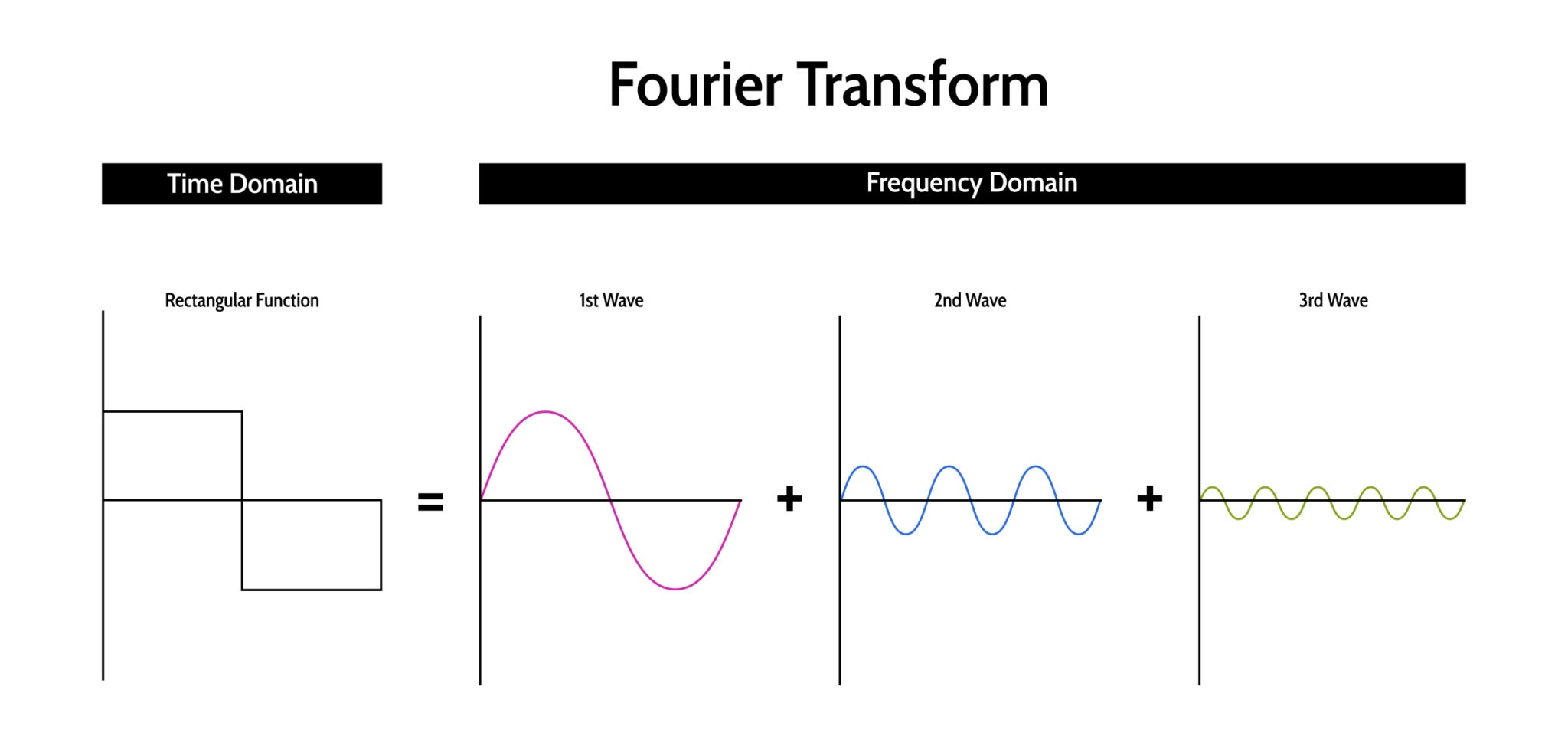
但傅里叶（Fourier）告诉我们：任何复杂的波形，都可以拆解成无数个正弦波的叠加。

FFT (Fast Fourier Transform) 就是那个拆解波形的“棱镜”。

  • X 轴： 频率 (Frequency)
  • Y 轴： 强度 (Magnitude)
  • 看到的是： 信号的“配方表”**。

![[Pasted image 20251213131958.png]]

1. 生活中的类比：果汁与配方

  • 时域信号： 一杯混合果汁（你只能喝出它酸酸甜甜，看到它是红色的）。
  • FFT 变换： 一张配方表。
    • 草莓：50%
    • 香蕉：30%
    • 苦瓜：5%（这就是干扰！）

2. CEMS 里的侦探故事

假设你的 $\text{SO}_2$ 读数一直在抖动，幅度 $\pm 1$ ppm。你用滤波怎么也滤不掉。

你对数据做了一个 FFT 分析，发现频谱图上有一根尖刺：

  • 案例 A：尖刺在 50Hz。
    • 破案： 50Hz 是市电频率。说明你的信号线没有屏蔽好，或者是电源地线没接好，工频干扰串进来了。
  • 案例 B：尖刺在 30Hz。
    • 破案： 你的切光轮电机转速正好是 1800rpm ($1800/60 = 30Hz$)。说明切光轮震动太大，引起了光路抖动。
  • 案例 C：尖刺在 0.5Hz。
    • 破案： 你的采样泵是不是每 2 秒钟“喘”一次气？这是蠕动泵或隔膜泵的脉动干扰。

结论： 在时域上，它们都是“乱跳”；但在频域上，它们都有“指纹”。FFT 是诊断仪器故障的神器。

第二章：手术刀式的切割 —— 数字陷波器 (Notch Filter)

当你用 FFT 找到了那个讨厌的 50Hz 工频干扰，下一步怎么办？

用普通的低通滤波（求平均）？

  • 缺点： 为了滤掉 50Hz，你会把 1Hz、2Hz 的有用信号也压制住，导致响应变慢。

这时候，你需要一把“激光手术刀”，只切除 50Hz 这一块肉，保留其他所有部分。 这就是 带阻滤波器 (Band-stop Filter)，如果阻带极窄，我们叫它 陷波器 (Notch Filter)。

  • 原理： 在数学上设计一个公式，让信号通过时，唯独 50Hz 的正弦波会被完全抵消（增益为 0），而 10Hz 或 100Hz 的信号无损通过。

第三章：Python 视觉盛宴 —— 抓出干扰并消灭它

我们来模拟一个真实的 CEMS 事故现场：

  1. 真实信号： 一个缓慢变化的 $\text{SO}_2$ 浓度。
  2. 干扰源： 50Hz 的强烈工频干扰（电源没接好）。
  3. 任务： 用 FFT 揪出它，然后用陷波器干掉它。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
from scipy import signal

# 配置中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# ==========================================
# 1. 制造案发现场 (生成信号)
# ==========================================
fs = 1000  # 采样率 1000Hz (每秒采1000个点)
T = 2.0    # 总时长 2秒
N = int(fs * T) # 总点数
t = np.linspace(0, T, N, endpoint=False)

# 真实信号：一个 2Hz 的缓慢波动 (模拟气体浓度变化)
sig_clean = 1.0 * np.sin(2 * np.pi * 2 * t)

# 干扰信号：50Hz 的强噪音 (模拟工频干扰)
noise_50hz = 0.5 * np.sin(2 * np.pi * 50 * t) 

# 白噪声：随机背景噪音
noise_white = np.random.normal(0, 0.2, N)

# 混合在一起：这就是 ADC 读到的烂数据
sig_corrupted = sig_clean + noise_50hz + noise_white

# ==========================================
# 2. 侦探环节 (FFT 频谱分析)
# ==========================================
yf = fft(sig_corrupted)       # 做傅里叶变换
xf = fftfreq(N, 1 / fs)       # 计算频率轴
# 我们只看前半部分 (正频率)
yf_abs = np.abs(yf[:N//2]) * 2 / N
xf_axis = xf[:N//2]

# ==========================================
# 3. 手术环节 (IIR 陷波器设计)
# ==========================================
# 设计一个针对 50Hz 的陷波器
# 质因数 Q 决定了切口有多窄。Q=30 表示切得很窄，不伤及无辜。
b, a = signal.iirnotch(w0=50.0, Q=30.0, fs=fs)

# 应用滤波器
sig_filtered = signal.filtfilt(b, a, sig_corrupted)

# ==========================================
# 4. 绘图展示
# ==========================================
plt.figure(figsize=(12, 10))

# 图1：时域波形对比 (乱糟糟 vs 干净)
plt.subplot(3, 1, 1)
plt.plot(t[:500], sig_corrupted[:500], 'r-', alpha=0.5, label='受污染的信号 (ADC原始)')
plt.plot(t[:500], sig_clean[:500], 'k--', linewidth=2, label='真实信号 (理想)')
plt.title("【时域】 案发现场：根本看不清真实信号", fontsize=14)
plt.legend(loc='upper right')
plt.grid(True)

# 图2：频域频谱 (破案证据)
plt.subplot(3, 1, 2)
plt.plot(xf_axis, yf_abs, 'b-')
plt.xlim(0, 100) # 只看 0-100Hz
plt.title("【频域】 侦探视角：FFT 抓到了！50Hz 处有巨大尖峰", fontsize=14)
plt.xlabel("频率 (Hz)")
plt.ylabel("强度 (Amplitude)")
plt.axvline(50, color='r', linestyle='--', label='发现 50Hz 干扰')
plt.axvline(2, color='g', linestyle='--', label='发现 2Hz 有用信号')
plt.legend()
plt.grid(True)

# 图3：滤波后效果 (手术成功)
plt.subplot(3, 1, 3)
plt.plot(t[:500], sig_filtered[:500], 'g-', linewidth=2, label='陷波器处理后')
plt.plot(t[:500], sig_clean[:500], 'k--', alpha=0.5, label='真实信号')
plt.title("【结果】 手术后：精准切除 50Hz，保留有用信号", fontsize=14)
plt.legend(loc='upper right')
plt.grid(True)

plt.tight_layout()
plt.show()

运行结果解读

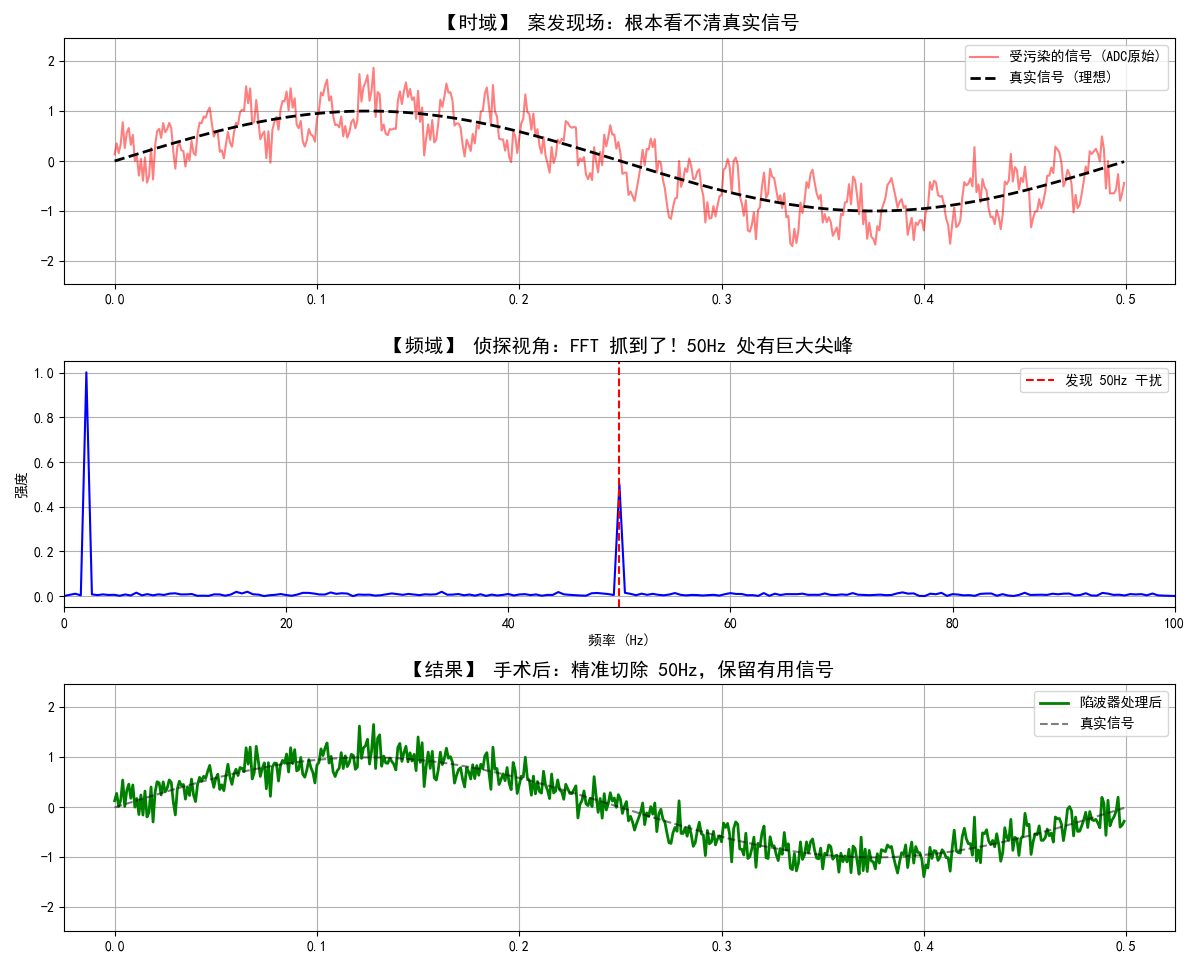
当你运行这段代码，你会看到三张图，讲了一个完整的故事：

  1. 第一张图（时域）： 你会看到红色的线毛毛糙糙的，上面叠加了密密麻麻的锯齿。你很难看清那条原本平滑的正弦波。这就是我们在现场看到的原始数据。
  2. 第二张图（频域 - 上帝视角）： 这是最震撼的一张。
    • 在 2Hz 的地方有一根柱子（这是我们要的信号）。
    • 在 50Hz 的地方有一根巨大的红柱子。
    • 真相大白： 原来让信号变脏的罪魁祸首就是 50Hz！
  3. 第三张图（滤波后）： 绿色的线（处理后）和黑色的虚线（真实值）几乎完美重合。
    • 注意：我们并没有用强力的平均滤波（那样会让波形滞后），我们只是“挖掉”了 50Hz。所以信号的反应速度丝毫没有变慢，但毛刺全没了。

总结

  • FFT (傅里叶变换)： 是诊断工具。它不改变信号，但能告诉你信号里有什么鬼（干扰源频率）。
  • 陷波器 (Notch Filter)： 是手术工具。当你用 FFT 确诊后，用陷波器可以精准切除特定频率的干扰，而不影响信号的灵敏度。
Licensed under CC BY-NC-SA 4.0
© 2024 - 2025 Coffity