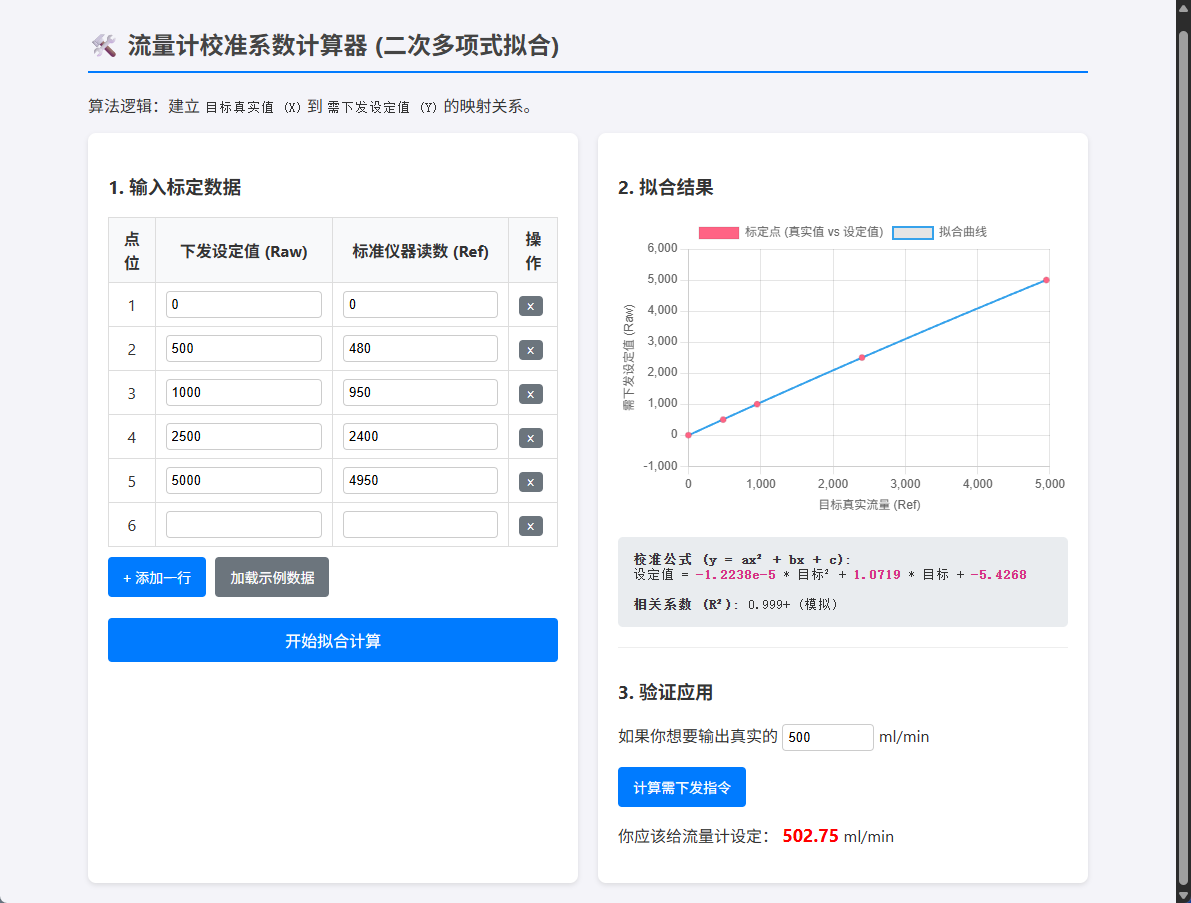
例如我有一个未校准过的流量计和一个校准过的流量计,通过通讯,让未校准过的流量计输出 500ml 气体,当然真是输出可能并非 500ml。此时校准过的流量计显示 480ml,那么可以未这个未校准过的流量计提供一个参考值。依此类推,500ml、1000ml、2500ml 等等这些点校准过的流量计都给出一个参考值。然后通过这些点位的参考值,可以给未校准过的流量计计算出校准系数。
这是工业仪表(特别是 MFC 质量流量控制器 或 气体稀释仪/配气仪)中非常标准的“多点标定” (Multi-point Calibration) 或 “线性化” (Linearization) 过程。这个过程通常分为三个步骤:数据采集、模型拟合、校准应用。
第一步:数据模型定义
我们定义两组数据序列:
- $X$ (未校准/原始值):你下发的设定值(Setpoint)或者仪表原始读数。
- 例如:$500, 1000, 2500$ mL/min
- $Y$ (参考值/标准值):标准流量计测得的真实值。
- 例如:$480, 990, 2480$ mL/min
我们的目标是找到一个函数 $f(x)$,使得 $Y \approx f(X)$。之后在实际使用时,如果读到了 $X$,我们就用 $f(X)$ 计算出真实的 $Y$;或者如果你想输出真实的 $Y$,你需要反算出应该设定的 $X$。
第二步:常用的三种算法实现
根据精度的要求和微处理器的计算能力,通常有以下三种方案:
方案一:分段线性插值法 —— 最常用、最稳健
这是在嵌入式底层(如 STM32, GD32)中最常见的做法。它不追求一条完美的曲线,而是把相邻的两个校准点连成直线。
原理:假设当前流量处于两个校准点之间:$(x_i, y_i)$ 和 $(x_{i+1}, y_{i+1})$。对于任意一个输入 $x$(在 $x_i$ 和 $x_{i+1}$ 之间),校准后的值 $y$ 计算公式为:$$y = y_i + (x - x_i) \cdot \frac{y_{i+1} - y_i}{x_{i+1} - x_i}$$
- 优点:计算简单,CPU 负担小,不会出现高阶多项式拟合在端点处的“龙格现象”(震荡)。
- 龙格现象 (Runge’s Phenomenon) :当你试图用过高阶数的多项式去完美穿过每一个校准点时,虽然曲线在这些点上是准的,但在头尾两端(边缘区域),曲线会发生剧烈的、完全不符合逻辑的震荡
- 缺点:在点与点之间是直线的,如果传感器非线性极强,需要更密集的校准点。
方案二:最小二乘法多项式拟合 —— 精度更高
如果你希望曲线更平滑,且校准点较多(例如 5-10 个点),可以使用多项式拟合。通常 2 次(抛物线) 或 3 次(S 型) 多项式就足够了。
原理:假设校准方程为:$$y = ax^2 + bx + c$$ 通过最小二乘法算法(Least Squares),输入所有的 $(X, Y)$ 点对,计算出系数 $a, b, c$。
- 优点:全局平滑,对热式流量计这种非线性传感器效果很好。
- 缺点:算法较复杂(涉及到矩阵运算),且如果校准点有误(坏点),会影响全局精度。
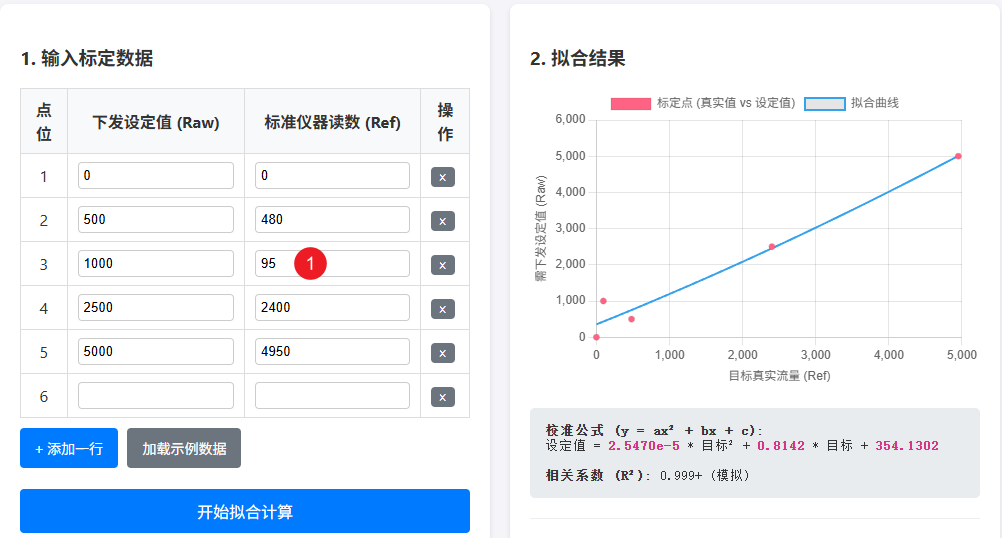
如果存在坏点,例如输入 950 的时候输入成 95 了,拟合出来的直线会影响全局精度
方案三:查表法 (Look-up Table)
这是方案一的简化版。如果不计算插值,而是建立一个巨大的数组(例如把 0-5000ml 分成 5000 个点),直接查表。但这太占内存,通常配合方案一使用。