ZZZ-21-串口通讯+VOFA

在工业开发（如 CEMS）中，VOFA+ 配合串口（UART）简直是“神兵利器”。它能把枯燥的数字变成实时的波形图，让你一眼看出传感器的数据稳不稳定、有没有噪声。

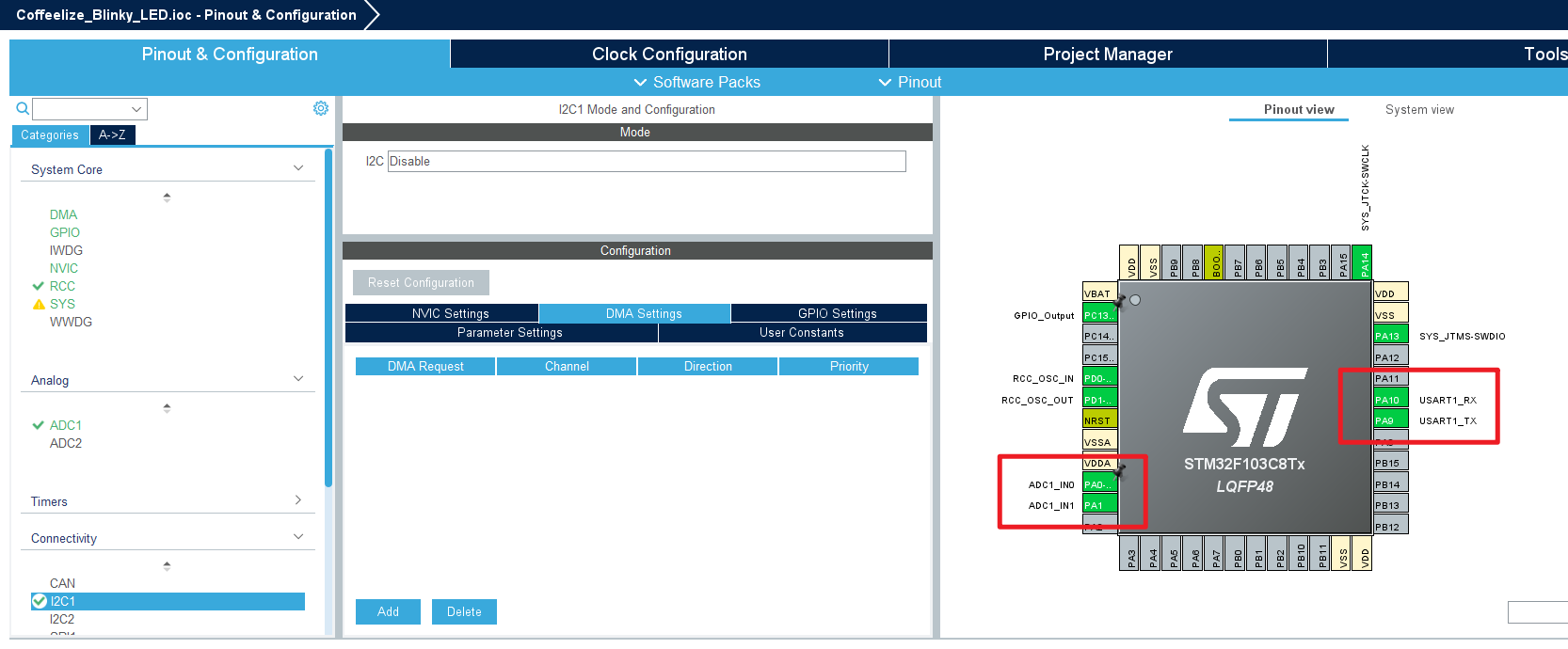
这里我们使用 ZZZ-18-ADC多通道采集、[[ZZZ-19-ADC采样数据滤波]] 中对单片机的配置【两个传感器、串口通讯、扫描模式 (Scan) + 循环模式 (Circular) + DMA】

编写代码 (main.c)

第一步：定义更大的缓冲区 

1
2
3
4
5
6

/* USER CODE BEGIN PV */
#define SAMPLES 10  // 每个通道采样 10 次
#define CHANNELS 2 // 共 2 个通道

uint16_t adc_buffer[SAMPLES * CHANNELS]; // 长度为 20 的数组
/* USER CODE END PV */

第二步：启动采集 

1
2
3
4
5
6
7
8

/* USER CODE BEGIN 2 */
// 为了精准，建议先进行 ADC 校准（F1系列特有＿
HAL_ADCEx_Calibration_Start(&hadc1);

// 核心命令：启势 ADC + DMA
// 参数：ADC句柄，存储的目标地址，要搬运的数据个数
HAL_ADC_Start_DMA(&hadc1, (uint32_t*)adc_buffer, SAMPLES * CHANNELS);
/* USER CODE END 2 */

第三步：数据平均处理并发送 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

/* USER CODE BEGIN WHILE */
  while (1)
  {
      uint32_t sum_A = 0;
      uint32_t sum_B = 0;

      // 1. 从 DMA 缓冲区计算平均值（让你看到的波形更平滑）
      for(int i = 0; i < SAMPLES; i++) {
          sum_A += adc_buffer[i * CHANNELS];     // 通道 A
          sum_B += adc_buffer[i * CHANNELS + 1]; // 通道 B
      }
      
      float volt_A = (float)sum_A / SAMPLES * 3.3f / 4095.0f;
      float volt_B = (float)sum_B / SAMPLES * 3.3f / 4095.0f;

      // 2. 核心步骤：按照 VOFA+ 的 FireWater 协议打印
      // 注意：末尾必须有 \n，VOFA+ 靠它来识别一帧数据的结束
      printf("%.3f,%.3f\n", volt_A, volt_B);

      // 3. 适当延时
      // VOFA+ 绘图能力很强，10ms~100ms 都可以。这里设为 20ms，波形会很丝滑
      HAL_Delay(20); 

    /* USER CODE END WHILE */

在 VOFA+ 的 FireWater 协议中，如何同时发送多个数据通道? 使用 printf 以逗号分隔数值，并以 \n 结尾。例如：printf("%f,%f\n", val1, val2);。

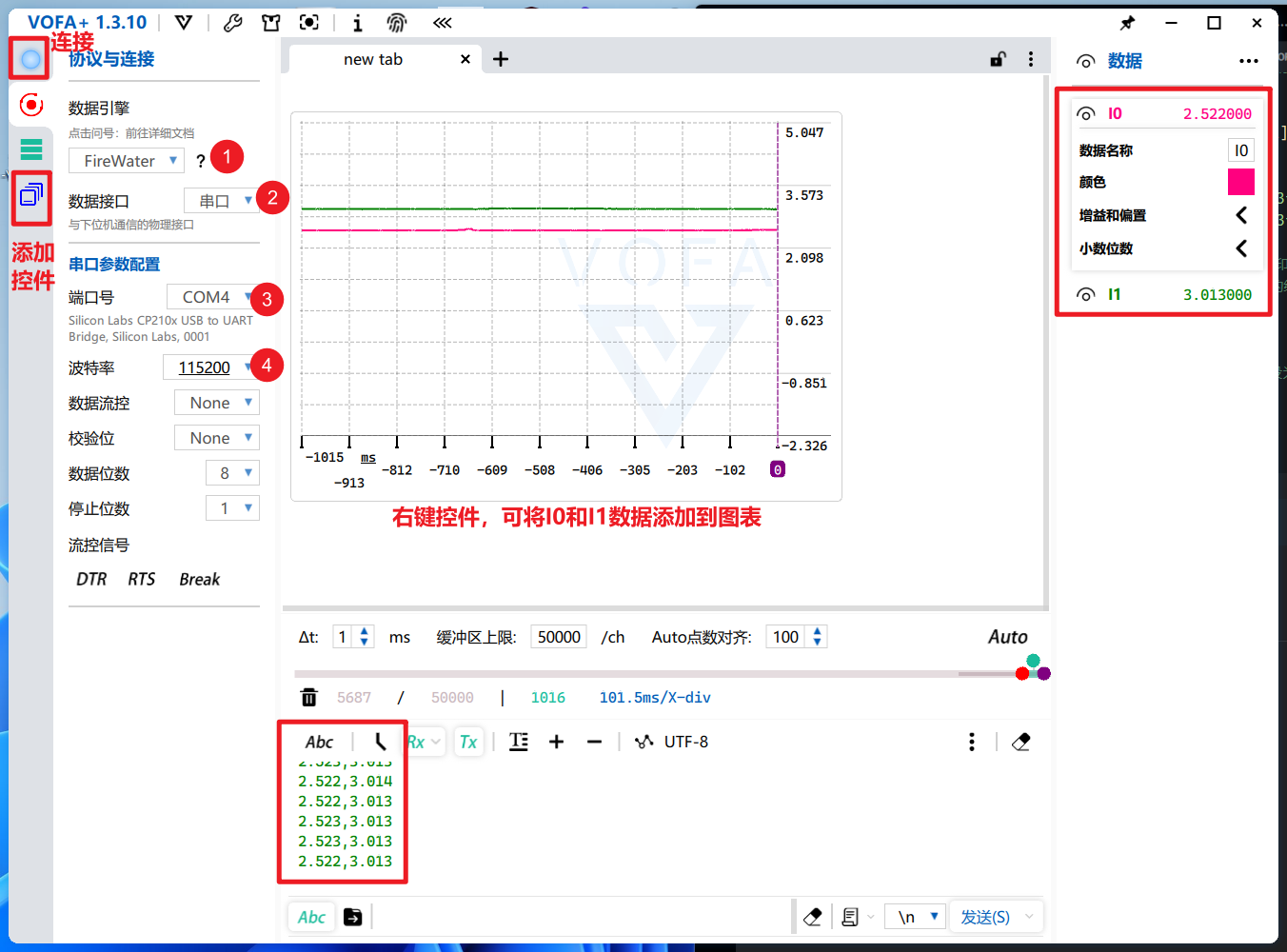
配置 VOFA+ 工具

  • 打开 VOFA+，点击左侧的“小齿轮”图标（设置）。
  • 数据引擎 (Data Engine)：选择 FireWater。
  • 连接配置：
    • 选择你的 COM 口（和烧录器/串口线对应）。
    • 波特率：检查你在 CubeMX 里的设置，通常是 115200。
  • 开始运行：点击右上角的红色圆圈（连接）。
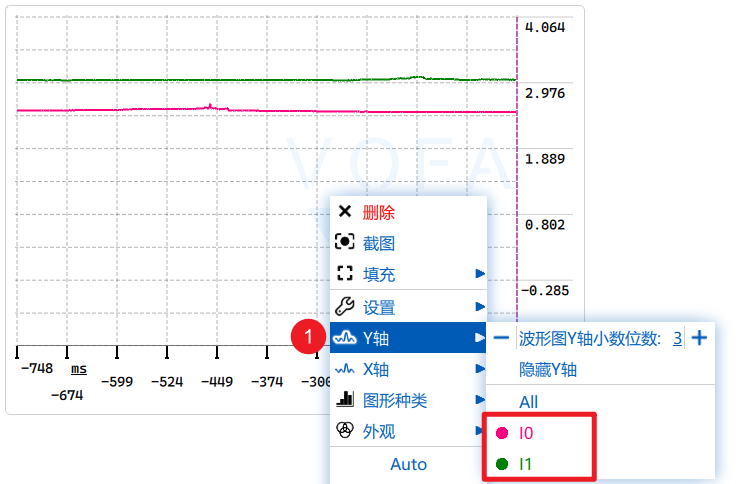
  • 添加波形图：
    • 右键点击空白处 -> 控件 -> Waveform（波形图）。
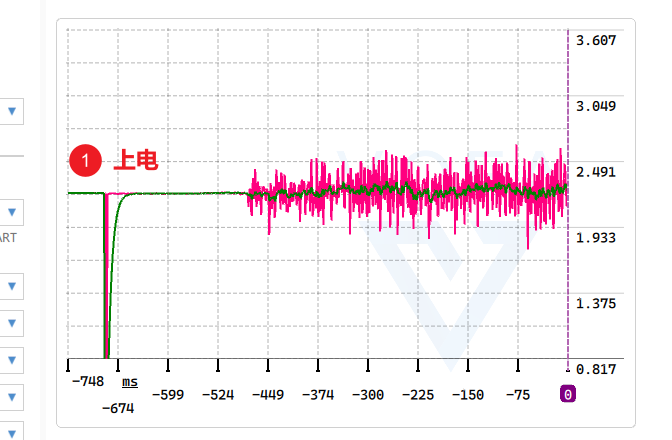
    • 此时你应该能看到两条线在跳动了！

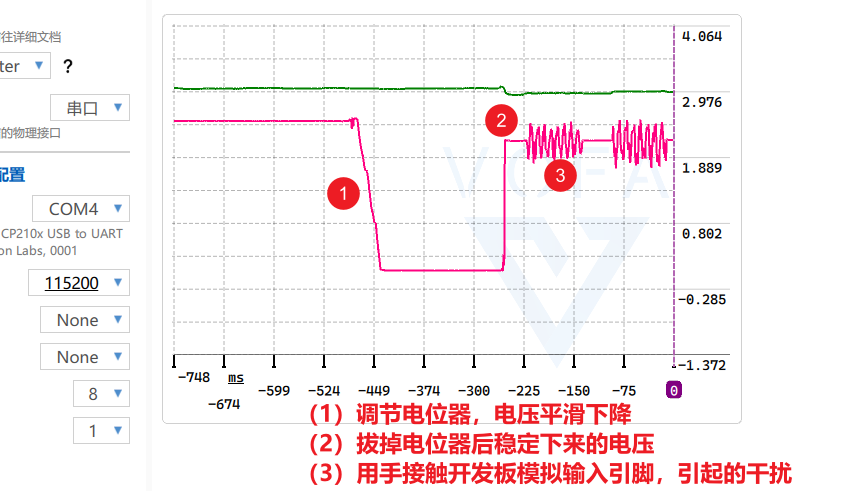
进阶挑战：工频干扰

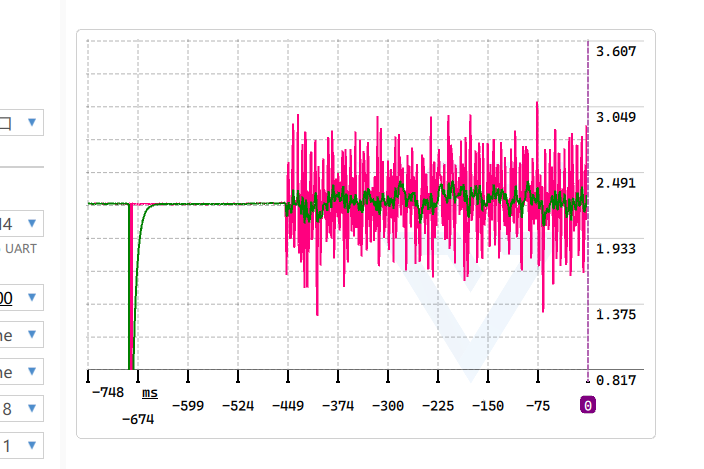
用手摸一下 ADC 的输入引脚，如（3）所示，波形因为人体感应电产生了剧烈的波动，这就是噪声，之后我们会用算法滤掉它

为什么会出现圈 (3) 的波动

你观察到的这个波动非常典型。当你的输入引脚（ADC 通道）处于高阻抗状态（比如拔掉了电位器，引脚悬空或者只由人体接触时），它就像一根“天线”，会吸收空间中的电磁干扰，最主要的就是环境中的 50Hz 市电工频干扰。

利用“算法”把这些毛刺“磨平”

为了应对你观察到的圈 (3) 这种干扰，工业界最常用的方案是 一阶滞后滤波 (First-order Lag Filter)。它比简单的算术平均值更节省内存，且波形更加平滑。

1. 滤波原理公式

$$Y(n) = \alpha \cdot X(n) + (1 - \alpha) \cdot Y(n-1)$$

  • $X(n)$：本次采样的原始值。
  • $Y(n-1)$：上一次滤波后的输出值。
  • $\alpha$：滤波系数（$0 < \alpha < 1$）。
    • $\alpha$ 越小，波形越平滑，但响应越慢；$\alpha$ 越大，波形越灵敏，但滤除噪声能力弱。

2. 代码实现

可以直接在 while(1) 循环上方定义一个静态变量来存储“上一次的值”，并应用这个公式。

1
2
3
4

  /* USER CODE BEGIN 1 */
  static float filter_volt_A = 0.0f;
  const float alpha = 0.15f; // 滤波系数，你可以尝试修改这个值观察 VOFA+ 上的变化
  /* USER CODE END 1 */

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

while (1)
{
	uint32_t sum_A = 0;
	uint32_t sum_B = 0;

	// 1. 计算平均值（作为原始输入值值）
	for(int i = 0; i < SAMPLES; i++) {
		sum_A += adc_buffer[i * CHANNELS];
		sum_B += adc_buffer[i * CHANNELS + 1];
	}

	// 计算当前这一刻的原始电压
	float raw_volt_A = (float)sum_A / SAMPLES * 3.3f / 4095.0f;
	float raw_volt_B = (float)sum_B / SAMPLES * 3.3f / 4095.0f;

	// 2. 核心算法：一阶滞后滤波（只对 A 进行处理作为演示）
	// 公式：本次输出 = alpha * 本次采样 + (1 - alpha) * 上次输出
	filter_volt_A = alpha * raw_volt_A + (1.0f - alpha) * filter_volt_A;

	// 3. 核心步骤：只用一个 printf，一次性发出三个数据
	// VOFA+ 会识别到 3 个通道：通道0(原始A), 通道1(滤波A), 通道2(原始B)
	printf("%.3f,%.3f,%.3f\n", raw_volt_A, filter_volt_A, raw_volt_B);

	// 4. 适当延时，20ms 对应 50Hz 的采样率，对观察干扰波形非常合适
	HAL_Delay(20);

  /* USER CODE END WHILE */
  • 红色为原始曲线【注意，这里没有用上面所说的一阶滞后滤波，但依然用了 [[ZZZ-19-ADC采样数据滤波]] 的平均滤波】
  • 绿色为滤波之后的曲线【相对于红色曲线多了一层一阶滞后滤波】

如果去掉 [[ZZZ-19-ADC采样数据滤波]] 中的平均滤波，直接使用一阶滞后滤波，效果如下

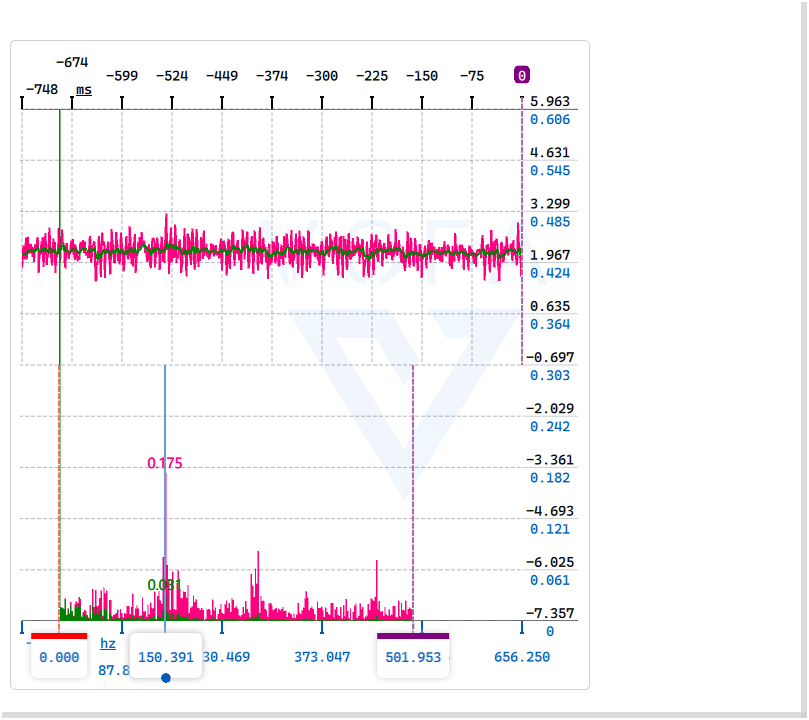
另外，还有一个值得学习的点是，如何根据频域图来找干扰（再 VOFA+ 中可以添加频域图）

数据的逻辑映射

掌握了 VOFA+，就相当于拥有了一双“电子显微镜”。我们可以利用这双眼睛，把你的 STM32 变成一个真正的工业测量仪表初级原型。

在 CEMS（烟气监测）领域，传感器很少直接告诉你“电压是多少”，它们通常输出的是 4-20mA 电流或 0-5V 电压，对应的是烟气浓度（比如 $0 \sim 100,mg/m^3$ 的 $SO_2$）。我们可以在代码中添加一些数学转换，让 VOFA 不再显示枯燥的电压，而是浓度

尝试编写一个“映射函数”

假设你正在模拟一个二氧化硫（$SO_2$）传感器：

  • $0.0V$ 对应 $0,mg/m^3$
  • $3.0V$ 对应 $100,mg/m^3$

你可以定义一个公式：$$Concentration = Voltage \times \frac{100}{3.0}$$

1
2
3
4
5

// 在 while(1) 里
float so2_conc = filter_volt_A * (100.0f / 3.0f); // 计算浓度

// 发送给 VOFA+：原始电压，滤波电压，SO2浓度
printf("%.3f,%.3f,%.3f\n", raw_volt_A, filter_volt_A, so2_conc);

在 VOFA+ 中观察

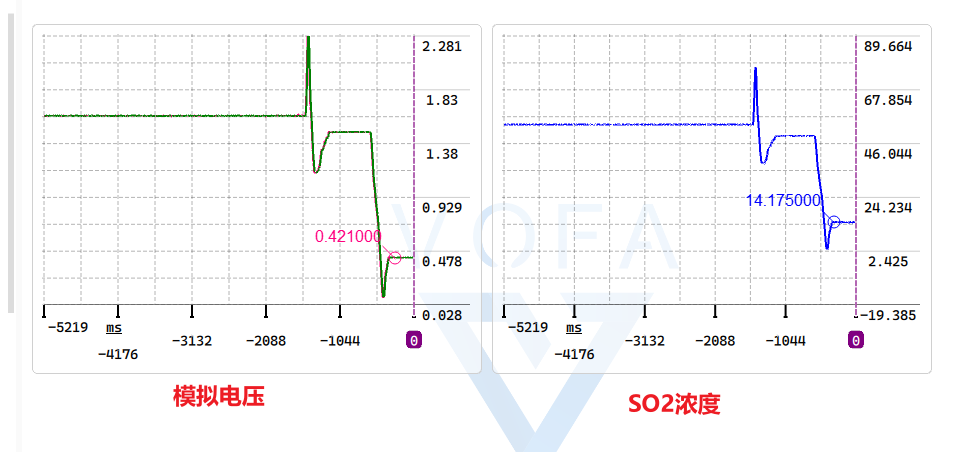
可以在 VOFA+ 里同时打开两个窗口：

  • 左边放波形图：看电压的平滑度。
  • 右边放“数字仪表盘” (Number 控件)：直接看当前的 $SO_2$ 浓度数值。当拨动电位器时，你会发现自己正在“调节”烟气浓度。

思考：为什么用 $3.0V$ 对应 $100,mg/m^3$

1、留出“安全冗余度”（Headroom）

在现实世界中，如果你的传感器满量程刚好是 $3.3V$，而你的单片机供电也是 $3.3V$，这会带来一个很尴尬的问题：削顶（Clipping）。

  • 如果传感器因为某种原因（比如瞬时超标）输出了 $3.35V$，你的 ADC 读出来依然是 $4095$（对应 $3.3V$）。这意味着你丢失了超标的那部分数据，且无法判断它是刚好满量程还是已经溢出了
  • 工程做法：通常会设计电路，让传感器的最大量程对应 ADC 满量程的 80%~90%（例如 $3.0V$）。这样即使信号稍微超出一点，单片机依然能捕捉到变化曲线。

2、电压波动风险

单片机的 $3.3V$ 电源往往不是完美的 $3.3000V$。

  • 如果此时电脑 USB 供电不足，电压降到了 $3.25V$。
  • 如果你以 $3.3V$ 为标准计算，所有的测量结果都会产生比例偏差。
  • 将满量程定在 $3.0V$，可以一定程度上降低对电源绝对精准度的依赖（当然，最专业的做法是使用内部或外部的参考电压基准）。

3、线性区的保护

大多数运算放大器（模拟信号处理电路）在接近电源轨（比如 $0V$ 或 $3.3V$）时，输出的线性度会变差。

  • 信号在 $0.5V \sim 2.8V$ 之间可能非常准，是一条直线。
  • 一旦到了 $3.2V$ 以上，曲线可能会变弯。
  • 思考：为了保证 数据的精准，我们宁愿只用中间那段最准的“黄金区间”。

总结：这就是“工程思维”

  • 数学思维：$3.3V / 4096$，追求理论的极致利用。
  • 工程思维：$3.0V / 4096$，追求系统的鲁棒性（稳定性）和容错率。

所以你会发现很多专业仪器在标定时，都会预留出 10% 的“超量程监测能力”，就是为了防止信号“顶到天花板”导致数据丢失

Licensed under CC BY-NC-SA 4.0
© 2024 - 2026 Coffity